3ª Clase (20/02/2013)

Hoy hemos comenzado repasando las ecuaciones diferenciales. Donde 

f(t,x(t))=dx/dt

 es una ecuación diferencial en forma explicita. Existen métodos para la resolución de este tipo de ecuaciones, nosotros utilizaremos los siguientes:

• Aplicando la transformada de Laplace (método matemático).
• Resolución numérica (método computacional).

La transformada de Laplace de una función f(t) definida para todos los números positivos t ≥ 0, es la función F(s), definida por:

 

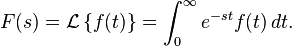
Este método consiste en despejar la x(s) siempre y cuando la integral este definida. Esta primera transformada nos sirve para pasar de f(t) a F(s), pero con la transformada inversas conseguimos lo contrario.

Esta transformada de Laplace tiene las siguientes propiedades:

• Linealidad
• Derivación
• Integración
• Teorema del valor inicial
• Teorema del valor final   
• etc 

 A continuación hemos demostrado la propiedad "Heaviside":

En el caso de que f sea lineal la ecuación diferencial queda de la siguiente forma:

                                                   dx/dt=ax(t) +bu(t)

Donde el siguiente sistema es de primer orden:

                                           a1*(dx/dt)+a0 *x(t)=bu(t)   

y el siguiente de segundo orden:

                                a2*(d^2x/dt^2)+ a1*(dx/dt)+a0 *x(t)=bu(t)

El método de la transformada de Laplace consiste en aplicar Laplace a ambos miembros de la ecuación:
 
Con lo que hemos conseguido despejar. null podemos la realizar la transformación inversa, en el programa matlab se haría mediante  la función "ilaplace" . A continuación se muestra una tabla de las transformadas de Laplace.